Wie funktioniert die Isochron-Methode

Wie funktioniert die Isochron-Methode?

Isochron-Datierung erfordert eine vierte Messung, in diesem Fall die Masse eines weiteren Isotops desselben Elements, das als Produkt des radioaktiven Zerfalls entsteht. (Aus Platzgründen werde ich das Mutter-Isotop als P, das Tocher-Isotop als D, und das nicht-radioaktive Isotop desselben Elements, alsD _ibezeichnen). Zusätzlich erfordert diese Methode, daß man Messungen von verschiedenen Objekten vornimmt, die alle zu derselben Zeit aus einem gemeinsamen Vorrat an Stoffen entstanden (Gesteine, die mehrere verschiedene Mineralien enthalten, eignen sich hierzu vorzüglich).

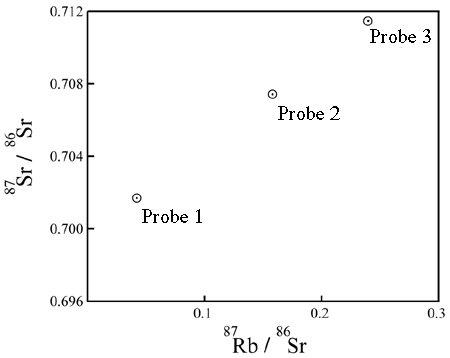
Jede dieser Messungen wird als Wert in einem Koordinatensystem eingetragen. Die X-Achse stellt das Verhältnis von PzuD _i dar. Die Y-Achse stellt das Verhältnis von DzuD _i dar. Ein Rb/Sr-Isochron-Graph sieht beispielsweise so aus:

P= ⁸⁷ Rb; D= ⁸⁷ Sr; D _i= ⁸⁶ Sr.

Abbildung 1: Beispiel für einen Isochron-Graphen.

Was sagt der Graph aus?

Ziel dieser graphischen Darstellung ist es, eine Korrelation zwischen

Der Menge an P (X-Wert der Daten), und
einer etwaigen Anreicherung D (Y-Wert der Daten):

festzustellen.

Abbildung 2: Bedeutung der Achsen des Graphen

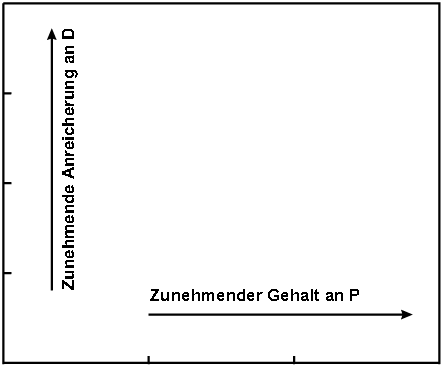
Wenn die Punkte auf einer Geraden liegen und die Gerade eine positive Steigung aufweist, zeigt das eine sehr starke Korrelation zwischen:

Der Masse von P in jeder Probe und
In welchem Maß sie an D , relativ zu D i, angereichert ist.

Das ist eine notwendige und erwartete Konsequenz, wenn das zusätzliche D ein Produkt des Zerfalls von P in einem geschlossenen System im Lauf der Zeit ist. Sie kann anders nicht vernünftig erklärt werden.

Warum liegen die Isochron-Daten auf einer Geraden?

Man würde erwarten, daß die Daten auf einer Gerade liegen, wenn bestimmte Ausgangsbedingungen gegeben waren. Betrachten wir ein geschmolzenes Gestein, in dem alle Atome (radioaktive und nicht radioaktive Isotope) homogen verteilt sind. Dessen Zusammensetzung würde in dem Diagramm als ein einziger Punkt erscheinen

Abbildung 3: Zusammensetzung der gesamten Schmelze

Wenn die Schmelze erstarrt, bilden sich Mineralien. Sie 'wählen' sich die Atome, die sie einbauen, aufgrund derer chemischen Eigenschaften

Weil DundD _i Isotope desselben Elements sind, haben sie identische chemische Eigenschaften. * Einzelne Mineralien können verschiedene Mengen dieses Elements enthalten, aber alle werden dasselbe Verhältnis D/D _i wie das Ausgangsmaterial enthalten. Daraus folgt ein identischer Y-Wert für alle Werte, unabhängig davon, welches Mineral sie repräsentieren (und der mit dem des Ausgangsmaterials übereinstimmt).

* Die obige Darstellung ist etwas vereinfacht. Es gibt geringe Unterschiede zwischen Isotopen desselben Elements, und unter relativ seltenen Umständen ist es möglich, daß eine gewisse Unterscheidung zwischen diesen erfolgt. Dieser Vorgang wird als Isotopenanreicherung bezeichnet. Dieser Effekt stellt fast immer eine sehr geringe Abweichung von einer homogenen Verteilung der Isotope dar. Das würde in etwa ausreichen, um einen Irrtum von etwa 0.002 Halbwertszeiten in einem Nicht-Isochronen-Alter zu erzeugen. (Das kann passieren ... aber es ist selten und der Effekt ist nicht groß genug, um die extrem hohen Alter angeblich junger Formationen zu erklären.)

P dagegen ist ein anderes Element mit unterschiedlichen chemischen Eigenschaften und wird daher anders als D& D _i verteilt werden, wenn sich die verschiedenen Mineralien bilden. Dadurch entsteht ein Bereich von X-Werten für die Meßwerte, die unterschiedliche Mineralien repräsentieren.

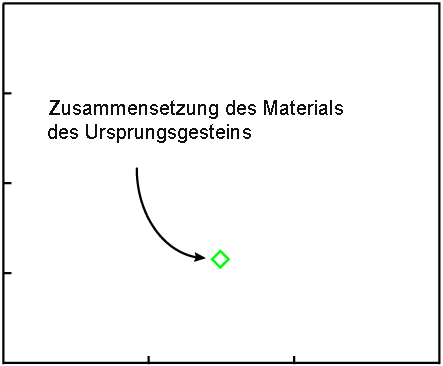
Weil die Koordinaten der Daten denselben Y-Wert und eine Reihe von X-Werten haben, liegen sie ursprünglich alle auf einer horizontalen Geraden:

Isochrone zum Zeitpunkt Null für die ursprünglichen Mineralien

Abbildung 4: Unterschiedlicher Einbau von Elementen, wenn sich die Mineralien bilden

Eine waagrechte Linie steht für ein "Null-Alter". *

* Genauer gesagt repräsentiert eine waagrechte Linie ein Alter, das von Null nicht unterschieden werden kann. In den meisten Fällen wird ein Alter von weniger als etwa 10 ^-3P Halbwertszeiten Null im Rahmen der Meßgenauigkeit einschließen. (Der Bereich der Ungenauigkeit ist unterschiedlich, er kann bis zu einer Größenordnung vom oben genannten Durchschnittswert abweichen. Er hängt in jedem Einzelfall von der Genauigkeit der Messung und davon ab, wie gut die erhaltenen Daten auf einer Geraden liegen.) Bei der Rb/Sr-Isochron-Datierung beispielsweise sind alle Alter von weniger als einigen Dutzend Millionen Jahren von Null nicht unterscheidbar. Das umfaßt die gesamte Junge-Erde-Zeitskala mehrtausendfach.

Wenn mehr Zeit vergeht und eine ausreichende Menge an radioaktiven Zerfällen erfolgt, nimmt die Menge an P um einen bestimmten Betrag in jeder Probe ab, während die Menge an D um den entsprechenden Betrag zunimmt. Im Diagramm bewegen sich daher die Koordinaten der Meßwerte nach links (abnehmende P Menge) und nach oben (zunehmende D Menge). Weil jedes Atom P zu einem Atom D zerfällt, werden sich die Koordinaten für den Meßwert jeder Probe auf einer Geraden mit der Steigung -1 verschieben.

Der Zerfall erfolgt proportional (das heißt, wenn 20% P in einer Probe zerfallen sind, werden 20% P in jeder Probe zerfallen sein). Daraus folgt, daß die Koordinaten der Meßwerte mit dem höchsten Gehalt an P (am weitesten rechts im Graphen) pro Zeiteinheit am weitesten verschoben werden. Die Daten bleiben zwar auf einer Geraden, wenn die Zeit fortschreitet, aber die Steigung der Geraden nimmt zu:

Abbildung 5: Verschiebung der Koordinaten der Meßwerte durch den Zerfall

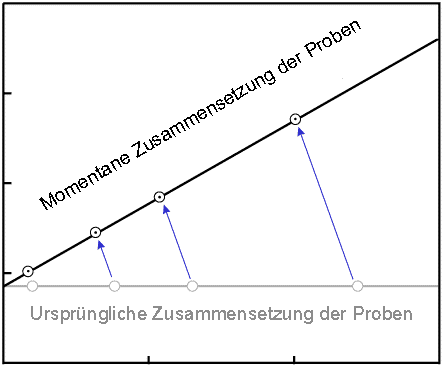
Die Steigung der Geraden ist das Verhältnis der Anreicherung Dzum verbleibenden P. Sie kann anstelle von " D _jetzt /P _jetzt " in die Zerfallsgleichung eingesetzt werden.

Einige Anmerkungen

"Unsicherheit" des Alters

Wenn eine "einfache" Datierung durchgeführt wird, erhält man eine einzige Zahl. Es gibt keinen vernünftigen Weg, anzugeben, wie dicht das errechnete Ergebnis beim wahren Alter liegt.

Ein weiterer Vorteil der durch Isochronen gemessenen Alter ist, daß eine "Unsicherheit" des Alters automatisch dadurch bestimmt wird, wie gut die Meßwerte auf einer Geraden liegen. Ein übliches statistisches Verfahren, das auf die Meßwerte angesetzt wird, liefert sowohl die Steigung der Ausgleichsgeraden (ein Alter) als auch eine Varianz in der Steigung (eine Unsicherheit des Alters). Je dichter die Daten an der Ausgleichsgeraden liegen, desto niedriger ist die Unsicherheit.

N ä here Informationen über das Erstellen einer Ausgleichsgeraden (auch Regressionsanalyse genannt), können Sie in folgenden Werken finden:

Gonick (1993, pp. 187-210), ein ausgezeichneter, allgemeinverständlicher Überblick.
York (1966), ein kurzer, fachlich orientierter Überblick. a short technical overview.
McIntyre et al. (1966), eine Diskussion einiger Anpassungen der Regressionsanalyse, mit deren Hilfe die Genauigkeit der Isochron-Datierung gesteigert werden kann.

Allgemeine Anmerkungen zu den "Grundannahmen zum Datieren"

Für alle radiometrischen Altersbestimmungen benötigt man, um zu genauen Altern zu kommen, bestimmte Ausgangsbedingungen und ein Fehlen von Verunreinigungen über den gesamten Zeitraum. Eine wundervolle Eigenschaft der Isochron-Methode ist: Wenn eine dieser Voraussetzungen nicht gegeben ist, ist es so gut wie sicher, daß die Meßwerte das dadurch anzeigen würden, daß sie nicht auf einer Geraden liegen. (Dieser Punkt wird viel ausführlicher weiter unten diskutiert werden.) Während die einfachen Methoden einfach ein falsches Alter ergeben würden, zeigen die Isochron-Methoden die fehlende Eignung eines Objekts für eine Altersbestimmung im allgemeinen an.

nächster
Abschnitt

voriger
Abschnitt

Übersicht